Davulun şeklini duyabiliyor musun?

Bu spektral geometri sorusunun cevabı, casusluktan kuantum yerçekimine kadar çok sayıda heyecan verici uygulamaya sahiptir. Ancak bugüne kadar matematik alanı hala birçok gizemi barındırıyor.
Bir nesneye çarptığınızda ses düzeninden çok şey öğrenebilirsiniz. Peki ses dalgaları gerçekte ne kadar bilgi içeriyor?
1966’da yayınlanan bir makalenin kulağa matematiksel olmayan bu başlığı, “Bir davulun şekli duyulabiliyor mu?”, matematiğin gelecek onyılları üzerinde belirleyici bir etkiye sahip olacaktı. Hatta sonunda konunun tamamen yeni bir alanını, seslerin geometrisini ele alarak açtı. Spektral geometri olarak adlandırılan geometri, ilginç casusluk tekniklerinden olası bir kuantum yerçekimi teorisine kadar şaşırtıcı uygulamalara sahiptir. Ancak bu güne kadar bu bölge hâlâ birçok gizemi gizliyor.
Temel sorun oldukça anlaşılır: Şampanya bardağına kaşıkla vurduğunuzda çıkan ses, kaşığı bira bardağına vurduğunuzda alacağınız sonuçtan önemli ölçüde farklı oluyor. Sadece camın kalınlığı değil aynı zamanda kabın şekli ve boyutu da rol oynar. Polonyalı matematikçi Mark Kac (1914–1984) da muhtemelen böyle düşünüyordu. Meslektaşı George Eugene Uhlenbeck’in 65. doğum gününü bir kaşık ve bardakla duyurmak yerine, ilgili matematik problemiyle uğraşmayı tercih etti ve “Davulun şekli duyulabilir mi?” adlı çalışmasını Uhlenbeck’e ithaf etti.
Kac’ın yayını, durumu eğlenceli bir şekilde anlatıyor; Ancak matematikçi bir çözüm sunamadı. O zamana kadar uzmanlar yalnızca tam tersi sorunu ele alıyordu: belirli bir şeklin sesini hesaplamak. Bu her zaman teorik olarak mümkün olsa da çoğu zaman çok karmaşık olduğu ortaya çıkar.
Titreşen bir dize
Ancak Kac tam tersi bir durumla ilgileniyordu. Bir nesnenin sesi onun geometrisini açığa çıkaracak kadar bilgi içeriyor mu? Bir boyutta durum kesinlikle böyledir. Bunun için her iki ucundan sabitlenen ve kopan tek bir ip hayal edebilirsiniz. Tel titreşmeye başlar, çevredeki havanın titreşmesine ve böylece bir ses oluşmasına neden olur.
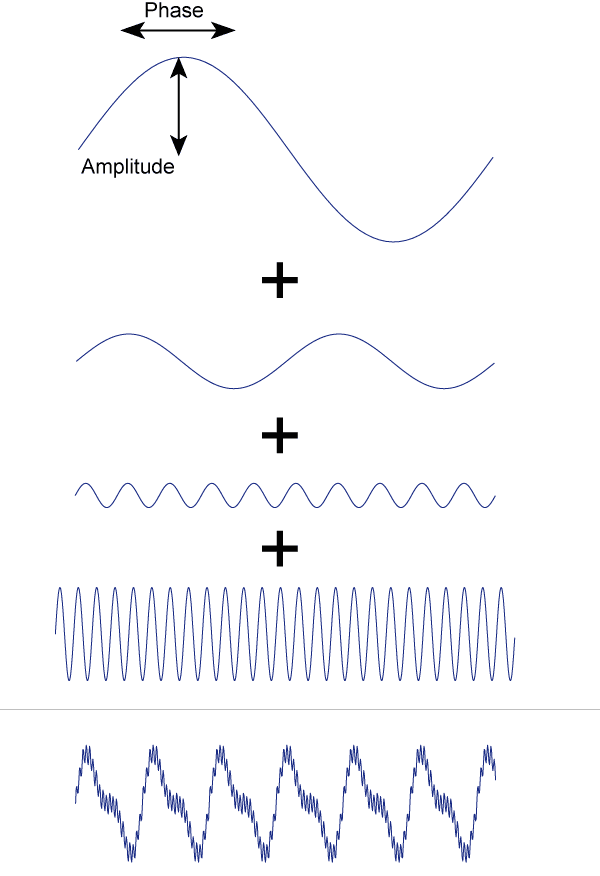
Fourier teoremi | Bir fonksiyon veya sinyal çok sayıda sinüs ve kosinüs fonksiyonunun toplamı olarak yazılabilir.
Bir ipin titreşimleri ilk bakışta oldukça karmaşık görünebilir. Ancak bunların sinüzoidal dalgaların süperpozisyonları olduğu ortaya çıktı. Fourier teoremi, her sinyalin – yani her titreşimin – basit sinüs eğrilerine bölünebileceğini belirtir. Bunları tek tek inceleyerek sinyalin tamamına dair her şeyi öğrenebilirsiniz.
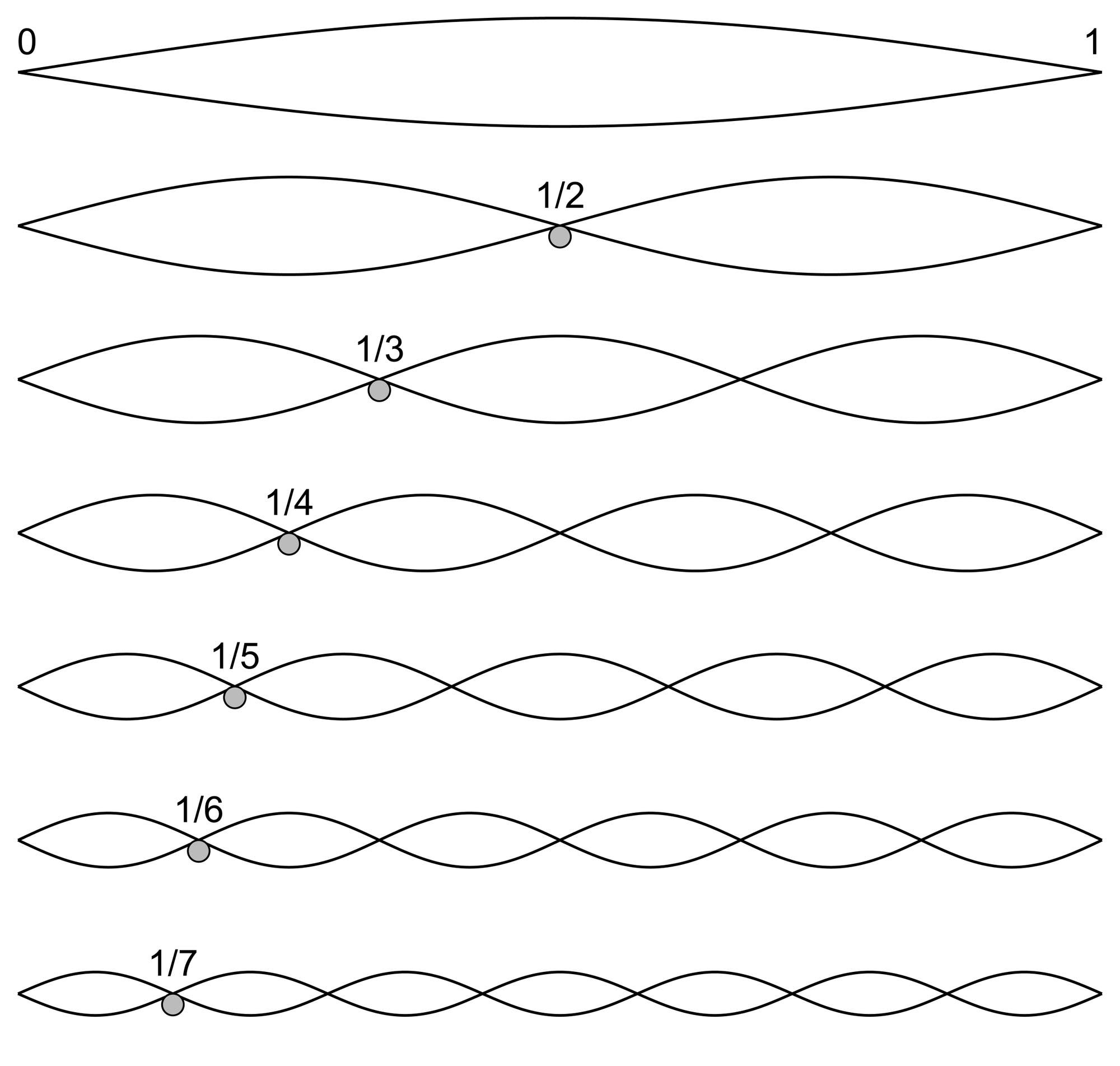
Temel ton ve imalar | Bir tel farklı frekanslarda titreşebilir. En düşük frekans (üst) temel tonu işaretler, diğer katkılar ise armonilere karşılık gelir.
En düşük frekansa (ve dolayısıyla en uzun dalga boyuna) sahip sinüs dalgası, temel tona karşılık gelir. Tüm yüksek tonlar üst tonlara karşılık gelir. Birlikte ele alındığında bu özellikler, örneğin bir enstrümanın karakteristik sesini yaratır. Telin uzunluğunu biliyorsanız, temel ve armonik tonların frekanslarını kolayca hesaplayabilirsiniz.
Ancak sorunun tersi de çözülebilir. Titreşen bir telin sesini kaydederseniz tek yapmanız gereken farklı frekansları parçalara ayırmak ve ardından telin geometrisi (bu durumda uzunluğu) hakkında sonuçlar çıkarmaktır. Temel tonun dalga boyunun yarısı telin uzunluğuna karşılık gelir. Ne kadar uzun olursa, temel tonu o kadar derin olur ve bunun tersi de geçerlidir.
Davul sesinin analizi
Kac, 1966 yılında yayınlanan çalışmasında davul sesiyle, yani kapalı, iki boyutlu bir yüzeyle ilgilenmişti. Örneğin dairesel bir davulun sesinin kare bir davuldan nasıl farklı olduğunu bilmek istiyordu. Üzerine membranın gerildiği yüzeyin şekline bağlı olarak sonucun farklı olacağını bekliyordu. Ve ses aslında yüzeyin boyutuna göre değişiyor; kare ve yuvarlak davullar da farklı tonlar üretiyor gibi görünüyor.
Ancak soru, her şeklin benzersiz bir ses üretip üretmediği veya aynı titreşim modellerinin ortaya çıktığı farklı yüzeylerin olup olmadığıdır. Tek boyutta bu imkansızdır: Temel trigonometri, her tel uzunluğunun benzersiz bir ton ürettiğini kanıtlamak için kullanılabilir. İki boyutta trigonometri artık yeterli değil; daha güçlü matematiksel silahlar ortaya çıkarmanız gerekiyor: daha yüksek analiz yöntemleri gerekiyor.
İki boyutlu dalga | İki boyutlu bir zarın salınımları aynı zamanda temel salınımlara da ayrılabilir.
Bir nesnenin sesi, dalga denklemi olarak adlandırılan çözümlerin sonucunda ortaya çıkar: Titreşimlerin bir yüzeye nasıl yayıldığını açıklar. Genel olarak bu, hem zaman hem de uzayda ikinci türevleri içeren bir diferansiyel denklemdir.
Görevi biraz basitleştirmek için uzmanlar sıklıkla bir numara kullanır: Tek boyutlu duruma benzer şekilde, bir titreşimi armonilerine ayırırlar. Temel olarak Fourier teoremini iki boyutta uygularsınız. Bu, çift zaman türevini bir sabitle değiştirmenize olanak tanır, böylece yalnızca uzaysal koordinatlardaki diferansiyel denklem kalır. Bu sabit, spektrum adı verilen sesin temel frekanslarını içerir.
Bir nesnenin şeklini biliyorsanız, dalga denklemini kullanarak ortaya çıkan titreşimleri ve dolayısıyla spektrumu hesaplayabilirsiniz. Bu karmaşıktır ancak prensipte mümkündür. Ancak tam tersine durum çok daha karmaşıktır. Bu, fizikçi Arthur Schuster’in 1882’de yazdığı şu sözlerle açıkça ortaya konmuştur: “Salınımlı bir sistemin yaydığı farklı tonları bulmak bazı özel durumlarda çözülebilir veya çözülemeyebilir. Ancak tam tersi problemi çözmek ve yaydığı seslerden zilin şeklini bulmak en yetenekli matematikçiyi bile şaşırtacaktır.”
Ses geometriyi açıkça belirtmiyor
1992’de, Kac’ın yayınlanmasından 25, Schuster’in açıklamasından 100 yıl sonra, Carolyn Gordon, David L. Webb ve Scott Wolpert, Kac’ın sorusuna bir yanıt buldular: Hayır, davulun şeklini duyamazsınız. Spektrum tek başına bir nesnenin geometrisini belirlemek için yeterli değildir. Üç matematikçi, çalışmalarında aynı spektrumu ve dolayısıyla aynı ses modelini üreten farklı geometrik şekillerin bir örneğini sunuyor.

İki tamburun spektrumu | Her iki form da (sağ ve sol) farklı olmasına rağmen aynı spektruma sahiptirler; dolayısıyla sesleri de aynıdır.
Kac’ın sorusuna artık genel bir yanıt bulunsa da sorunun kesin ayrıntıları hâlâ belirsizliğini koruyor. Örneğin hangi durumlarda ses bir nesnenin geometrisini belirlemek için yeterlidir. Uzmanlar, aynı spektruma sahip farklı şekillerin örneğini bulmak için son derece uzun bir süre araştırma yapmak zorunda kaldı. Ancak çoğu durumda ses benzersiz görünür.
Çünkü sesleriyle açıkça tanımlanan şekiller vardır: örneğin üçgenler, yamuklar veya paralelkenarlar. Genel olarak ses spektrumundan simetrik şekillerin geometrisini çıkarmak mümkün görünüyor. Bu, Gordon, Webb ve Wolpert’ın bulduğu karşı örnek türünün “kural mı yoksa istisna mı” olduğu sorusunu gündeme getiriyor. Şu ana kadar her şey ikincisine işaret ediyor gibi görünüyor” diye yazdı matematikçi Michael M. Bronstein liderliğindeki araştırmacılar 2018’de.
2023 yazında araştırmacılar bu alanda önemli ilerleme kaydetmeyi başardılar. Kac’ın bahsettiği soruna doğrudan değinmediler, bunun yerine Macar matematikçi George Pólya’nın 1954’te yaptığı bir varsayımı ele aldılar. Bu, bir formun belirli bir frekansın altındaki tüm armonilerinin sayısını tahmin ediyordu. Ancak yarattığı denklemin doğru olduğuna dair kanıtı yoktu. 1961’de Pólya, formülünün bir düzlemi boşluk olmadan kaplayabilen tüm yüzeylere (örneğin kareler, dikdörtgenler, üçgenler veya altıgenler) uygulanabileceğini kanıtlayabildi.
Çözüm çok fazla soyut matematik gerektirir
Diğer geometrik şekillerin de Pólya’nın varsayımını karşılayıp karşılamadığı neredeyse 70 yıl boyunca bir sır olarak kaldı. Ancak Haziran 2023’te Montréal Üniversitesi’nden matematikçi Iosif Polterovich ve ekibi, çemberlere ilişkin varsayımı doğrulamayı başardılar: Dairesel davulları titreştirirseniz, belirli bir frekansın altındaki armonilerin sayısı Polyá’nın formülü kullanılarak tahmin edilebilir.
Bu tür problemleri çözmek çok fazla soyut matematik gerektirse de ilgili uygulamalar doğası gereği oldukça pratiktir. Örneğin 2013 yılında araştırmacılar, dışbükey bir çokgene karşılık geldiği sürece tek bir tonun yankılanmasına dayanarak bir odanın şeklini belirleyebileceklerini gösterdiler. Dolayısıyla bu tür yöntemler casusluk teknikleri olarak kullanılabilir. Aslında, tam tersi sorun daha da yararlı: Uzmanlar artık titreşen bir çip torbasının video kayıtlarından sesleri geri yükleyebiliyor ve bu şekilde, insanları görmek zorunda kalmadan bir konuşmayı görsel olarak dinleyebiliyorlar.
Waterloo Üniversitesi’nden fizikçi Achim Kempf, tamamen farklı bir uygulama alanını araştırıyor: Dört temel kuvveti birleştirecek bir kuantum yerçekimi teorisi geliştirmek için spektral geometriyi kullanmak istiyor. Buradaki fikir, evrenimizin geometrisini anlamak için uzay-zaman içindeki kuantum fiziksel salınımları kullanmaktır. Ancak bu tamamen farklı bir zorluktur.
Matematikçilerin benim piyanonun sesini (tonu) nasıl hesaplayacaklarını merak ediyorum.!

Bir yanıt yazın